Movimiento circular

Hemos visto cómo dibujar una recta entre dos puntos (o como hacer que algo se mueva en línea recta). Vamos a ver ahora cómo dibujar un círculo punto a punto, que se podría aplicar para imitar un movimiento circular.

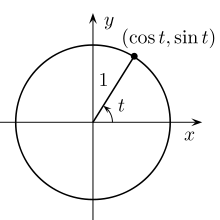
Las ecuaciones de cada punto X e Y de una circunferencia, a partir de su radio (r) y del ángulo (t) que forma ese punto con la horizontal son:

x = r · cos t

y = r · sin t

Si el centro de la circunferencia no es (0,0) sino otro punto de coordenadas (xCentro, yCentro), quedaría:

x = xCentro + r · cos t

y = yCentro + r · sin t

Si aplicamos esto a un fuente con Basic256, podría quedar así:

xCentro = 200
yCentro = 150
radio = 50
clg
for i = 1 to 360
plot xCentro + radio * cos(radians(i)), yCentro + radio * sin(radians(i))
pause (0.01)
next i

Sólo dos consideraciones:

• Normalmente "a un humano" le resulta cómodo medir en grados, pero las funciones "seno" (sin) y "coseno" (cos) suelen esperar que se indique el ángulo en radianes, por lo que habrá que convertir, usando órdenes como "DEG" (trabajar en grados), funciones como "radians" (convertir a grados, como en el ejemplo anterior) o bien convertir "a mano" de radianes a grados, multiplicando por 180 y dividiendo entre PI.
• Si los dos radios (horizontal y vertical) no son iguales, obtendremos una elipse en lugar de una circunferencia.